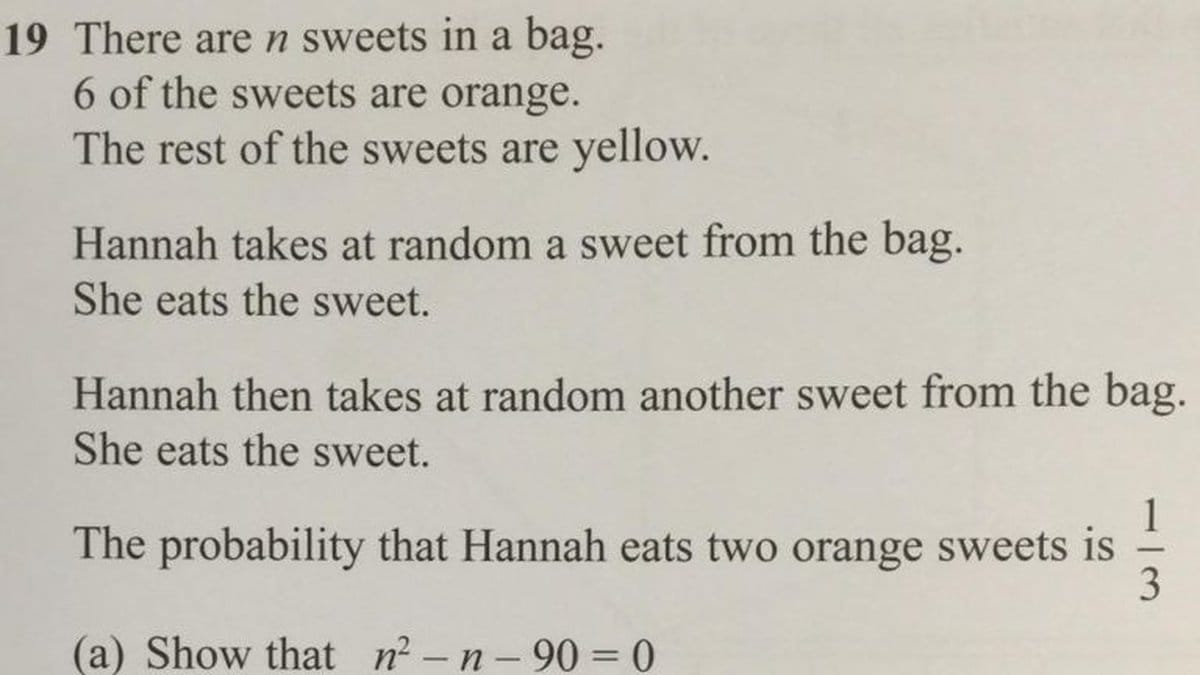Här är lösningen på "omöjliga" problemet
Pallar du inte mer? Här är svaret.
Okej. Nu kör vi.
Sammanlagt finns det n godisar i påsen, varav 6 stycken är orangea. Om hon tar en, är chansen 6/n att godisen hon får upp är orange. Om hon tar upp en, finns det en orange godis mindre och en godis mindre totalt.
Om hon tar en orange godis till skulle sannolikheten vara (6-1)/(n-1)=5/n-1
Nu tar vi reda på sannolikheten om hon får 2 orangea godisar genom att multiplicera bråket så här:
6/n*5/n-1=30/n²-n
Nu står det klart att sannolikheten att Hannah får upp två orangea godisar är 1/3, alltså 1/3=30/n²-n
Nu måste vi hitta den gemensamma nämnaren, då gör du bara så att du multiplicerar 1/3 med 30/30 vilket blir 30/90.
Om 30/90=30/n²-n, så är n²-n=90. Om n²-n=90 så har du bevisar att n²-n-90 är lika med 0.
Lätt som en plätt va?
